Machine Learning - 1.2 - Model and Cost Function
Bài thứ 2 trong chuỗi bài viết tự học Machine Learning Trong bài này, ta sẽ tìm hiểu về cost function, một function nhằm dự đoán giá trị output với một bộ các giá trị input/output cho trước.
Xem các bài viết khác tại Machine Learning Course Structure
1. Các ký hiệu
Chúng ta sẽ thống nhất 1 cách sử dụng các ký hiệu để biểu thị các thuộc tính của một bài toán.
x(i) sẽ là giá trị đầu vào, cũng được gọi là
input feature.y(i) sẽ là đầu ra mà ta cố dự đoán.
Một cặp (x(i), y(i)) được gọi là một
training example.Số lượng
training exampleđược gọi làm. Như vậy, i=1,2,3,…,m
Lưu ý rằng (i) chỉ là index của giá trị, không phải số lũy thừa
Ta dùng ký tự
X,Yđể biểu thị vùng không gian của input và outputVí dụ:
X = Y = ℝ
Khi đưa ra một bộ dữ liệu training (training set), mục tiêu của chúng ta là tạo ra được 1 function h sao cho h(x) có thể dự đoán gần đúng nhất giá trị của y.
hlà viết tắt cho từ Hypothesis, lý do cho tên gọi này chỉ đơn thuần là vì xưa kia, người ta đặt tên cho nó như vậy, và nó chết tên luôn.
Như vậy, process của chúng ta sẽ như sau:
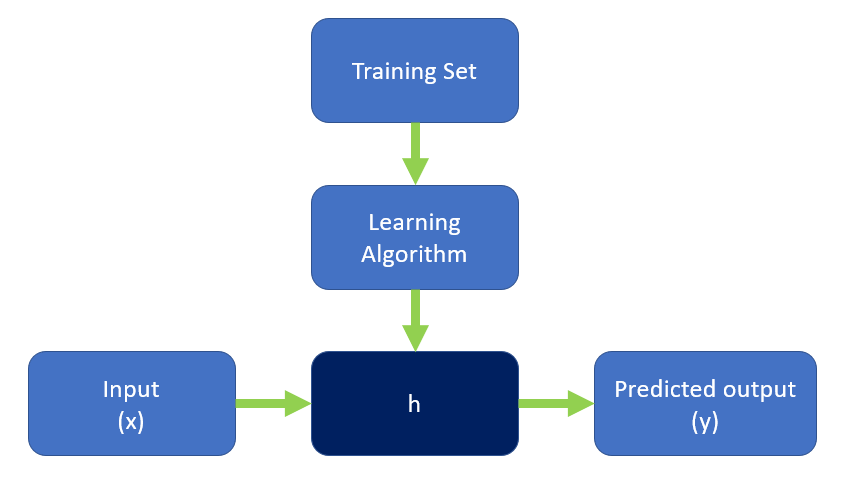
Khi y là một giá trị liên tục, ví dụ như giá nhà, giá cổ phiếu, thì đây là một regression problem.
Khi y chỉ là một số lượng nhỏ các giá trị nhất định (true/false - yes/no), thì đây là một classification problem.
2. Cost Function
Chúng ta “tính toán” sự chính xác của hàm hypothesis bằng cách sử dụng 1 hàm số. Hàm số đó gọi là cost function.
Trước khi đưa ra bất kỳ một công thức hay hàm số nào, hãy cùng tôi đào bới trong mớ kiến thức hỗn độn mà tôi chắc rằng sẽ giúp bạn hiểu ra nội dung cốt lõi của
Cost Function.
2.1. Toán học
2.1.1. Xác xuất và thống kê (Probability and Statistic)
Trong xác xuất thống kê, có một khái niệm gọi là Gaussian Distributed.
Đúng rồi, bạn không nhìn nhầm đâu.
Gaussiancũng là một tính năng nổi tiếng của…Photoshop, khi mà nó làm nhiễu đi vùng được chọn. Tính năng đó gọi làGaussian Blur.
Trong lý thuyết xác xuất, phân phối chuẩn, hay còn gọi là phân phối Gauss, phân phối Gaussian, phân phối Laplace-Gauss, là một dạng phân phối xác xuất liên tục (Continuous probability distribution).
Sở dĩ tôi nhắc tới phân phối chuẩn là bởi vì theo định lý giới hạn trung tâm (Central limit theorem), ở dạng tổng quát nhất của phân phối chuẩn, phân phối của tổng rất nhiều biến ngẫu nhiên độc lập sẽ có phân phối xấp xỉ chuẩn.
Tức là, số lượng training example càng nhiều thì mỗi một training example sẽ có giá trị càng gần với hàm hypothesis của chúng ta.
Tóm lại, ta sẽ chọn tham số sao cho khoảng cách từ đồ thị của hàm hypothesis tới y của các training example là ngắn nhất.
2.1.2. Phương sai (Variance)
Trong lý thuyết xác suất và thống kê, phương sai của một biến ngẫu nhiên là một độ đo sự phân tán thống kê của biến đó, nó hàm ý các giá trị của biến đó thường ở cách giá trị kỳ vọng bao xa.
Theo định nghĩa này của phương sai, đồ thị biểu diễn các giá trị kỳ vọng chính là đồ thị hàm hypothesis của chúng ta đó. Phương sai chính là giá trị mà ta muốn nó càng nhỏ càng tốt
Phương sai của một biến ngẫu nhiên là bình phương của độ lệch chuẩn.
Như đã nói ở phần trước, khi mà tập giá trị đầu vào training example của chúng ta đủ lớn, thì ta có thể xem mỗi training example là một biến ngẫu nhiên có phân phối chuẩn.
Vậy ta có:
Tập hợp kỳ vọng = hypothesis
$h_\theta(x)=\theta_0+\theta_1x$
Độ lệch chuẩn:
$latex h_\theta(x^{(i)})-y^{(i)}$
Phương sai = (độ lệch chuẩn)2
Vậy phương sai của tập hợp các training example sẽ là:
$latex \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$
Nhiệm vụ của ta là tìm ra giá trị nhỏ nhất của công thức trên.
2.2. Đạo hàm (Derivative)
Để tìm giá trị lớn nhất / nhỏ nhất của một hàm số, ta có thể sử dụng đạo hàm.
2.2.1. Một ví dụ toán học
Một trái banh được ném lên trời. Độ cao của trái banh so với mặt đất tại bất kỳ thời điểm t nào được tính bởi công thức:
h = 3 + 14t -5t2
Vậy độ cao lớn nhất của trái banh là bao nhiêu?
Ứng dụng đạo hàm, ta giải bài toán này như sau:
$latex \frac{\text{d}}{\text{d}t}h=0+14-5(2t)=14-10t$
Hàm số trên biểu thị mức độ thay đổi của độ cao h tại thời điểm t. Như vậy, tại độ cao lớn nhất, _mức độ thay đổi độ cao h = 0 (vì trái banh không tiếp tục bay cao lên nữa mà bắt đầu rơi xuống).
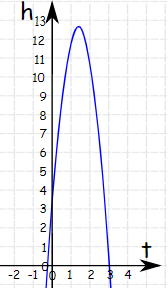
Vậy ta có:
[code lang=text] 14-10t = 0
=> t = 1.4 [/code]
Vậy độ cao lớn nhất là
[code lang=text] h = 3 + 14x1.4 - 10x1.4x1.4 = 12.8 [/code]
2.2.2. Lớn nhất hay nhỏ nhất
Làm sao ta biết được một hàm số sẽ có giá trị lớn nhất hay nhỏ nhất? Nếu dựa vào đồ thị thì quả là một cách tốn nhiều thời gian và công sức.
Tại đây, ta tiếp tục sử dụng đạo hàm (một lần nữa):
[code lang=text] f’(t) = 14 - 10t với t = 1.4 thì f’(t) = 0
=> f’’(t) = -10 với t = 1.4 thì f’’(t) = -10 [/code]
Đây gọi là Second Derivative Test, phát biểu như sau:
Khi một hàm số có mức độ thay đổi = 0 tại điểm x, thì giá trị hàm đạo hàm lần 2 của hàm số đó tại x nếu:
Nhỏ hơn 0: đó là giá trị lớn nhất.
Lớn hơn 0: đó là giá trị nhỏ nhất.
Bằng 0: chưa thể tìm được giá trị lớn nhất/nhỏ nhất của hàm số.
2.3. Công thức
Áp dụng cả 2 phần đạo hàm và toán bên trên, ta sẽ có:
$latex \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$
với
$latex h_\theta(x^{(i)}) = \theta_{0} + \theta_{1}x^{(i)}$
Lý do của số 2 dưới mẫu số là để triệt tiêu khi ta làm đạo hàm. Nhìn chung, nó không ảnh hưởng tới kết quả, vì mục tiêu là tìm giá trị nhỏ nhất của hàm số trên.
Vậy ta sẽ tìm giá trị của $latex \theta_{0}$ và $latex \theta_{1}$ để hàm số trên nhỏ nhất.